Алгебра Примеры
Геометрической прогрессией называется такая последовательность чисел , что каждый следующий ее элемент получается из предыдущего умножением на некоторое фиксированное число , называемое знаменателем прогрессии. Приведем еще три важные формулы, касающиеся геометрической прогрессии, которые необходимо знать наизусть: 1. Формула -го члена общего члена прогрессии.
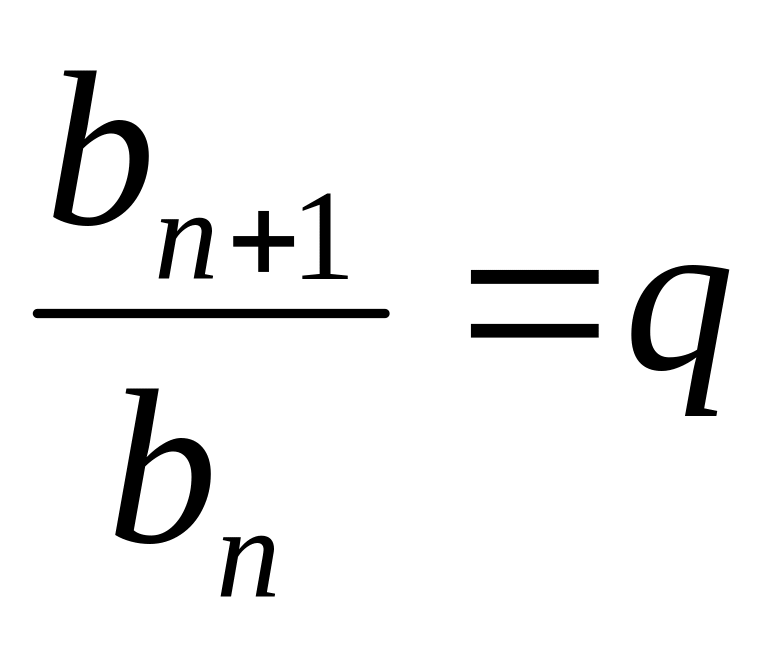
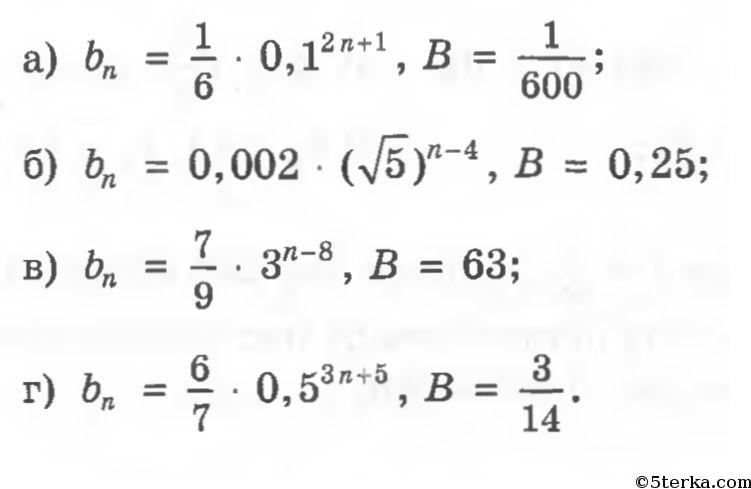
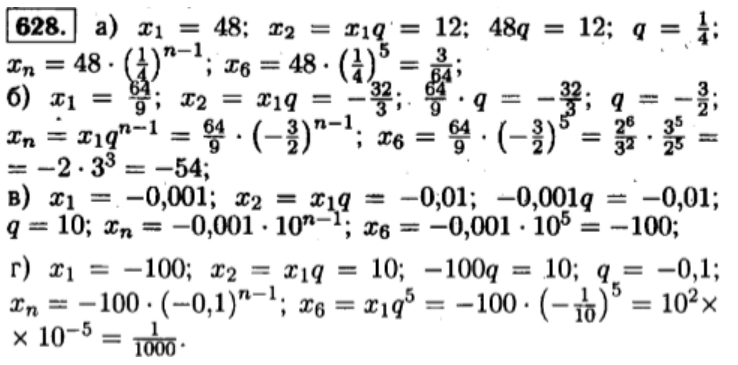
Если каждый член геометрической прогрессии больше предыдущего, то прогрессия называется возрастающей ; если меньше предыдущего, то убывающей. Геометрическая прогрессия называется бесконечно убывающей [2] , если знаменатель прогрессии по абсолютной величине меньше единицы. Однако это не только свойство, но и признак геометрической прогрессии , формулировка которого звучит следующим образом:. Последовательность положительных чисел тогда и только тогда является геометрической прогрессией, когда каждый её член, начиная со второго, есть среднее геометрическое предшествующего и последующего членов. Данный признак можно расширить на другие случаи. Это означает, что справедлива теорема:.
.gif "Урок 4: Определение геометрической прогрессии: формула n-го члена прогрессии")
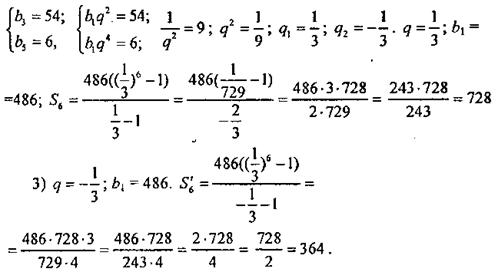
На сайте уже есть калькулятор для геометрической прогрессии — Геометрическая прогрессия , который позволяет найти сумму ее членов. Однако бывает еще и другая задача — по двум заданным соседним членам геометрической прогрессии найти знаменатель и ее первый член. Понятно, что в такой постановке задачи речь идет о возрастающей геометрической прогрессии, первый член которой, также как и знаменатель, являются целыми числами. Со знаменателем все понятно, два соседних члена геометрической прогрессии связаны соотношением , откуда. А вот чтобы получить первый член, надо делить каждый предыдущий на q, пока не перестанут получаться целые значения. Последнее целое значение и будет первым членом геометрической прогрессии.
